Siguiendo con la profundización en los fenómenos de debate esgrimidos en la colaboración que hice sobre la erística, esta vez, me gustaría instruiros en una de las herramientas más importante a la hora de debatir: la lógica. Siendo esta de una importancia muy característica, rara vez se usa, y rara vez se aplica para analizar la estructura de debate de los contendientes. En muchos casos, percibimos las proposiciones y conclusiones planteadas como válidas y tras deliberación mental, podemos estar más o menos de acuerdo con las conclusiones siguiendo un esquema de proposiciones aparentes conectadas entre sí de forma interesante. Sin embargo, esta vez vamos a aprender las normas básicas, la simbología y algunos ejemplos para asentar o repasar los contenidos aquí representados y/o aprendidos.
Definición
La lógica proposicional es un sistema de proposiciones que afirman o niegan una o varias proposiciones que pueden ser puestas a condición o ser directamente afirmadas. Así, cada uno de los elementos obedecerá y se tomarán de forma absoluta: es decir, cada proposición y condición inherente a ella se tomará de forma absoluta según la característica formal de este tipo de lógica. Así, por ejemplo, la lógica proposicional no incluye todas aquellas falacias que puedan darse en el lenguaje semántico, sino que utilizará siempre proposiciones verdaderas y llegará a conclusiones verdaderas según las proposiciones antedichas. En definitiva, la lógica proposicional nos sirve como herramienta dialéctica para llegar a la verdad o a la realidad material más evidente de forma correcta ante proposiciones absolutamente verdaderas, en una realidad material y cambiante. Unos de los exponentes más notables de la lógica proposicional y la lógica en general, son las matemáticas y su aplicación práctica: la física. La lógica proposicional pertenece al lenguaje científico y el marxismo, como ciencia, no es una excepción y su conocimiento resulta interesante para los estudiantes marxistas e incluso para los doctos en esta materia como instrumento de argumentación.
Simbología
Tomo de Wikipedia un cuadro que me ha parecido muy interesante y que nos servirá para aprender rápidamente los conectores lógicos. Existen más, aunque estos, son los más importantes y los que se utilizan en la inmensa mayoría de los casos, incluso, en razonamientos de gran envergadura:
Reglas de la lógica proposicional
1. La lógica proposicional siempre obedece a proposiciones absolutas. La utilización intencionada o no de falacias y enunciados materialmente falsos no son previstos por esta lógica y son motivo de estudio de la lógica informal.
2. La lógica proposicional sigue una estructura jerárquica y escalonada. En el lenguaje hablado y su transcripción escrita, podemos encontrarnos que los enunciados están escritos en párrafos, frases y en definitiva, textos; sin embargo, en la lógica proposicional formal, las proposiciones deben ser escalonadas y obedeciendo un orden jerárquico de relevancia que los podrá separar en paréntesis, llaves y corchetes.
3. La negación de la negación es la afirmación (¬¬p → p). La negación de la negación de la negación es la negación (¬¬¬p → ¬p). Esta regla nos sonará de las matemáticas elementales, donde menos por menos es más y menos por menos por menos, es menos; al igual que menos por más, siempre será menos y a la inversa.
4. Todos los elementos de las distintas proposiciones por regla general se escribirán en minúsculas. (p → q) y no (P → Q)
5. El verbo ser en sus distintas formas nos indica implicación o conclusión. Decir "ser" es decir "implica".
6. Siempre que queda una proposición aislada en una premisa, esta concluye en el escalón inferior a través del último símbolo que quede. Si es un condicional, entonces, un condicional; si es una disyunción, entonces una disyunción, si un bicondicional, entonces, un bicondicional. Si no hay ningún símbolo, entonces, siempre utilizaremos un condicional (→). Si la premisa termina en negación (¬) toda la premisa siguiente deberá ser negada.
7. Se cumple la regla de proporcionalidad al tratarse de términos absolutos; si ladra, es un perro, o, si es un perro, entonces ladra. (p → q) → (q → p)
8. Recuerda, la lógica proposicional sigue una jerarquía, entre el signo dentro de un conjunto y el signo que pueda englobar una totalidad o uniones de totalidades, prevalece el signo exterior siempre y cuando quede solo un elemento dentro del subconjunto. Al quedar solo, los conectores dentro del subconjunto desaparecen.
9. Cuando concluimos un sistema proposicional, deberemos colocar una linea debajo de la última proposición o bien en su lateral
derecho escribiendo la conclusión final. Lo más recomendable es escribir la conclusión en la vertical, pero también es posible formularla horizontalmente:

Aplicación de la lógica proposicional
Conocida la simbología y las principales normas de la lógica proposicional, pondremos en práctica esta simbología y como construir nuestro primer sistema proposicional de forma correcta, sencilla y aprenderemos como resolverlo.
Tomo del usuario PequeñoBurgués una frase suya escrita en este hilo para este propósito:
La construcción proposicional sería la siguiente:

Esto es una construcción sencilla, unas proposiciones que en orden jerárquico implican otra. Esta es una fórmula y una regla absoluta en términos de lógica formal. Esta es la construcción más sencilla en la que solo se forma en total una premisa. Una premisa es cada uno de los escalones de la secuencia lógica. La forma más fácil de poner a prueba una premisa es a través del silogismo, que consiste en dos premisas (o dos escalones) y una conclusión. Luego, si se da que el usuario se va por las ramas y empieza a pegar artículos, se concluye que cualquier cosa sin desmontar el planteo previo es malo para el debate y pasa a hacer el ridículo:

No siempre vamos a encontrar conclusiones que se organicen en una misma premisa, sino que tendremos que aplicar estas normas en sistemas lógicos más complejos y que nos obligarán a tomar lápiz y papel para resolverlo. Por supuesto, mis aplausos para aquellas predilectas que puedan resolver ingentes estructuras con facilidad, rapidez y con una calculo mental ejemplar.
Tomemos otro ejemplo, algo más complejo. Esta vez lo tomamos del usuario MolotoK del mismo hilo indicado anteriormente y en el que explicaremos determinadas formulaciones de la regla que no están explicítamente explicadas en la tabla de Wikipedia.

Recomiendo resolver los sistemas proposiciones de dos a dos e ir simplificando en la resolución de este a llegar a una conclusión irreductible.
Este ejemplo puede causar dudas, ya que algunas disyunciones no fueron catalogadas como tales, como por ejemplo:
· es acumular más apoyo social o popular que su contrario: ese "o" se refiere a la misma cosa. No es una disyunción entre dos entidades, sino una disyunción entre dos cualidades o intenciones del verbo y se utiliza la frase entera.
· y para hacerlo usan esas contradicciones a su favor: cuando se dan razones utilitarias, utilizamos una conclusión -como se ha hecho en el ejemplo-. Acumular más apoyo social o popular implica usar esas contradicciones a su favor. (a → c)
· O dicho de otra forma: es un ejemplo parecido al primer punto; quiere decir la misma cosa de forma distinta; la entidad principal se expresa de forma distinta, por lo que no es una conjunción entre dos entidades distintas.
Ejercicios con soluciones
¡Pongamos en práctica lo aprendido! A continuación, para asentar y demostrar que hemos aprendido los conocimientos anteriormente explicados, os propongo una serie de ejercicios basada en dos tipos: pasar textos a lógica proposicional y resolver estructuras de lógica proposicional. Las soluciones a estos ejercicios se mostrarán tras los ejercicios planteados ocultos en un spoiler. Se recomienda que se hagan primero todos los ejercicios y luego, se cotejen, ya que las soluciones aparecen seguidas; pueden utilizar las letras que os parezca, lo importante es la estructura lógica; os recomiendo utilizar un papel.
1. Pasa las siguientes frases a lógica proposicional
B) Si yo me compro un zapato, entonces lo habré pagado / Comprar un zapato implica pagarlo
C) Negar la negación que niega negar es negar el negar. Negar el negar.
2. Resuelve el siguiente sistema proposicional

Definición
La lógica proposicional es un sistema de proposiciones que afirman o niegan una o varias proposiciones que pueden ser puestas a condición o ser directamente afirmadas. Así, cada uno de los elementos obedecerá y se tomarán de forma absoluta: es decir, cada proposición y condición inherente a ella se tomará de forma absoluta según la característica formal de este tipo de lógica. Así, por ejemplo, la lógica proposicional no incluye todas aquellas falacias que puedan darse en el lenguaje semántico, sino que utilizará siempre proposiciones verdaderas y llegará a conclusiones verdaderas según las proposiciones antedichas. En definitiva, la lógica proposicional nos sirve como herramienta dialéctica para llegar a la verdad o a la realidad material más evidente de forma correcta ante proposiciones absolutamente verdaderas, en una realidad material y cambiante. Unos de los exponentes más notables de la lógica proposicional y la lógica en general, son las matemáticas y su aplicación práctica: la física. La lógica proposicional pertenece al lenguaje científico y el marxismo, como ciencia, no es una excepción y su conocimiento resulta interesante para los estudiantes marxistas e incluso para los doctos en esta materia como instrumento de argumentación.
Simbología
Tomo de Wikipedia un cuadro que me ha parecido muy interesante y que nos servirá para aprender rápidamente los conectores lógicos. Existen más, aunque estos, son los más importantes y los que se utilizan en la inmensa mayoría de los casos, incluso, en razonamientos de gran envergadura:
- Tablas de la simbología lógica proposicional:
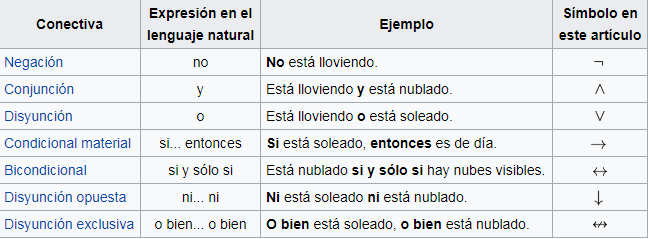
Fuente: pincha aquí
Reglas de la lógica proposicional
1. La lógica proposicional siempre obedece a proposiciones absolutas. La utilización intencionada o no de falacias y enunciados materialmente falsos no son previstos por esta lógica y son motivo de estudio de la lógica informal.
2. La lógica proposicional sigue una estructura jerárquica y escalonada. En el lenguaje hablado y su transcripción escrita, podemos encontrarnos que los enunciados están escritos en párrafos, frases y en definitiva, textos; sin embargo, en la lógica proposicional formal, las proposiciones deben ser escalonadas y obedeciendo un orden jerárquico de relevancia que los podrá separar en paréntesis, llaves y corchetes.
3. La negación de la negación es la afirmación (¬¬p → p). La negación de la negación de la negación es la negación (¬¬¬p → ¬p). Esta regla nos sonará de las matemáticas elementales, donde menos por menos es más y menos por menos por menos, es menos; al igual que menos por más, siempre será menos y a la inversa.
4. Todos los elementos de las distintas proposiciones por regla general se escribirán en minúsculas. (p → q) y no (P → Q)
5. El verbo ser en sus distintas formas nos indica implicación o conclusión. Decir "ser" es decir "implica".
6. Siempre que queda una proposición aislada en una premisa, esta concluye en el escalón inferior a través del último símbolo que quede. Si es un condicional, entonces, un condicional; si es una disyunción, entonces una disyunción, si un bicondicional, entonces, un bicondicional. Si no hay ningún símbolo, entonces, siempre utilizaremos un condicional (→). Si la premisa termina en negación (¬) toda la premisa siguiente deberá ser negada.
7. Se cumple la regla de proporcionalidad al tratarse de términos absolutos; si ladra, es un perro, o, si es un perro, entonces ladra. (p → q) → (q → p)
8. Recuerda, la lógica proposicional sigue una jerarquía, entre el signo dentro de un conjunto y el signo que pueda englobar una totalidad o uniones de totalidades, prevalece el signo exterior siempre y cuando quede solo un elemento dentro del subconjunto. Al quedar solo, los conectores dentro del subconjunto desaparecen.
9. Cuando concluimos un sistema proposicional, deberemos colocar una linea debajo de la última proposición o bien en su lateral
derecho escribiendo la conclusión final. Lo más recomendable es escribir la conclusión en la vertical, pero también es posible formularla horizontalmente:

Aplicación de la lógica proposicional
Conocida la simbología y las principales normas de la lógica proposicional, pondremos en práctica esta simbología y como construir nuestro primer sistema proposicional de forma correcta, sencilla y aprenderemos como resolverlo.
Tomo del usuario PequeñoBurgués una frase suya escrita en este hilo para este propósito:
PequeñoBurgués escribió:Que el usuario se va por las ramas y empieza a pegar artículos, o cualquier cosa sin desmontar el planteo previo no solo es malo para el debate si no que básicamente pasa a hacer el ridículo.
La construcción proposicional sería la siguiente:

Esto es una construcción sencilla, unas proposiciones que en orden jerárquico implican otra. Esta es una fórmula y una regla absoluta en términos de lógica formal. Esta es la construcción más sencilla en la que solo se forma en total una premisa. Una premisa es cada uno de los escalones de la secuencia lógica. La forma más fácil de poner a prueba una premisa es a través del silogismo, que consiste en dos premisas (o dos escalones) y una conclusión. Luego, si se da que el usuario se va por las ramas y empieza a pegar artículos, se concluye que cualquier cosa sin desmontar el planteo previo es malo para el debate y pasa a hacer el ridículo:

No siempre vamos a encontrar conclusiones que se organicen en una misma premisa, sino que tendremos que aplicar estas normas en sistemas lógicos más complejos y que nos obligarán a tomar lápiz y papel para resolverlo. Por supuesto, mis aplausos para aquellas predilectas que puedan resolver ingentes estructuras con facilidad, rapidez y con una calculo mental ejemplar.
Tomemos otro ejemplo, algo más complejo. Esta vez lo tomamos del usuario MolotoK del mismo hilo indicado anteriormente y en el que explicaremos determinadas formulaciones de la regla que no están explicítamente explicadas en la tabla de Wikipedia.
MolotoK escribió:Pero como ya he advertido atrás, el estilo de Jordi es el debate ideológico. Este es un debate donde los participantes tienen posturas ideológicas diferentes, y el objetivo NO es buscar la verdad resolviendo contradicciones, es acumular más apoyo social o popular que su contrario; y para hacerlo usan esas contradicciones a su favor. O dicho de otra forma: No quiere convencer a los participantes de nada, quiere convencer a los lectores anónimos, sean asiduos o casuales.

Recomiendo resolver los sistemas proposiciones de dos a dos e ir simplificando en la resolución de este a llegar a una conclusión irreductible.
Este ejemplo puede causar dudas, ya que algunas disyunciones no fueron catalogadas como tales, como por ejemplo:
· es acumular más apoyo social o popular que su contrario: ese "o" se refiere a la misma cosa. No es una disyunción entre dos entidades, sino una disyunción entre dos cualidades o intenciones del verbo y se utiliza la frase entera.
· y para hacerlo usan esas contradicciones a su favor: cuando se dan razones utilitarias, utilizamos una conclusión -como se ha hecho en el ejemplo-. Acumular más apoyo social o popular implica usar esas contradicciones a su favor. (a → c)
· O dicho de otra forma: es un ejemplo parecido al primer punto; quiere decir la misma cosa de forma distinta; la entidad principal se expresa de forma distinta, por lo que no es una conjunción entre dos entidades distintas.
Ejercicios con soluciones
¡Pongamos en práctica lo aprendido! A continuación, para asentar y demostrar que hemos aprendido los conocimientos anteriormente explicados, os propongo una serie de ejercicios basada en dos tipos: pasar textos a lógica proposicional y resolver estructuras de lógica proposicional. Las soluciones a estos ejercicios se mostrarán tras los ejercicios planteados ocultos en un spoiler. Se recomienda que se hagan primero todos los ejercicios y luego, se cotejen, ya que las soluciones aparecen seguidas; pueden utilizar las letras que os parezca, lo importante es la estructura lógica; os recomiendo utilizar un papel.
1. Pasa las siguientes frases a lógica proposicional
Mariano Rajoy escribió:A) un vaso es un vaso y un plato es un plato
Fuente: pinche aquí
B) Si yo me compro un zapato, entonces lo habré pagado / Comprar un zapato implica pagarlo
C) Negar la negación que niega negar es negar el negar. Negar el negar.
Constitución española de 1978 escribió:Artículo 92.
D) 1. Las decisiones políticas de especial trascendencia podrán ser sometidas a referéndum consultivo de todos los ciudadanos.
2. El referéndum será convocado por el Rey, mediante propuesta del Presidente del Gobierno, previamente autorizada por el Congreso de los Diputados.
3. Una ley orgánica regulará las condiciones y el procedimiento de las distintas modalidades de referéndum previstas en esta Constitución.
Fuente: pincha aquí
- Soluciones del ejercicio 1:

Luego, las decisiones políticas de especial trascendencia implican la convocación por parte del rey del referéndum que implican la aprobación del congreso, lo que implica una ley orgánica que regulará las condiciones y el procedimiento de las distintas modalidades del referéndum previstas en esta constitución si se convoca el referéndum consultivo Nota: como las implicaciones o condiciones son proporcionales entre sí, se puede alterar el orden de la conclusión ya que no importa el orden de la frase para decir la misma cosa: si se convoca el referéndum, entonces una ley orgánica regulará las condiciones y el procedimiento de las distintas modalidades de este
2. Resuelve el siguiente sistema proposicional

- Solución del ejercicio 2:






